Цікавая геаметрыя

30. Геаметрычныя падарожжы

Геаметрыя - адна з найбольш старажытных матэматычных навук. Першыя геаметрычныя факты мы знаходзім у вавілонскіх клінапісных табліцах і егіпецкіх папірусах (III тысячагоддзе да н.э.), а таксама ў іншых крыніцах.

Карткі вавілонскага клінапісу і егіпецкага папірусу. 

Назва навукі «Геаметрыя» - старажытнагрэчаскага паходжання. Яна складзена з двух старажытнагрэцкіх слоў: ge - «Зямля» і metreo - «мераю». Геаметрыя, як і многія іншыя навукі, паўстала з практычных патрэбаў людзей. На ранніх стадыях развіцця чалавецтва пры вырабе прылад працы і будаўніцтве жылля з'явілася неабходнасць вызначаць форму і памеры прадметаў. Дайшоўшыя да нас помнікі культуры і шматлікія пісьмовыя дакументы сведчаць пра тое, што ўжо каля 4000 гадоў таму жыхары Старажытнага Егіпта і Вавілона былі знаёмыя з асноўнымі законамі геаметрыі. 

Знакамітыя егіпецкія піраміды (грабніцы фараонаў) адрозніваюцца дзіўнай правільнасцю формаў. Значыць, іх будаўніцтвам кіравалі людзі, якія валодалі глыбокімі ведамі ў галіне геаметрыі. У старажытнаегіпецкіх папірусах, якія адносяцца да 2000-1700 гг. да н.э., змяшчаецца рашэнне шэрагу геаметрычных задач, прычым некаторыя з іх рэшаны бездакорна. Шмат для развіцця геаметрыі зрабілі навукоўцы Старажытнай Грэцыі.

Першыя доказы геаметрычных фактаў звязваюць з імем Фалеса Мілецкага (625-547 гг. да н.э.)

Аўтарам доказаў многіх тэарэм называюць Піфагора (564-473 гг. да н.э)

Абагульняючы вопыт вучоных старажытнай эпохі, можна адказаць на пытанне: «Што вывучае Геаметрыя?» Геаметрыя вывучае ўласцівасці геаметрычных фігур. 

Звычайна геаметрычныя фігуры з'яўляюцца мадэлямі аб'ектаў размешчаных вакол нас.

31.Геаметрычныя задачы на ​​вычэрчванне фігур без адрыву алоўка ад паперы

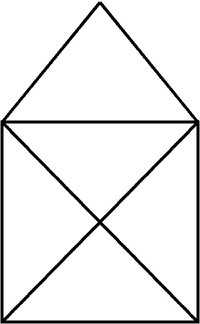
Напэўна, усе памятаюць з дзяцінства, што вельмі папулярная была наступная задача: не адрываючы алоўка ад паперы і не праводзячы па адной лініі двойчы, начарціць "адкрыты канверт": Паспрабуйце начарціць "адкрыты канверт".

 

Як вы бачыце, што ў некаторых атрымліваецца, а ў некаторых не. Чаму гэта адбываецца? Як правільна чарціць, каб атрымалася? І для чаго гэта патрэбна? 

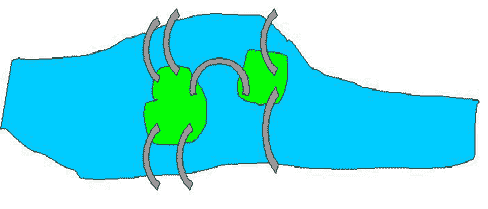
Адзін гістарычны факт. Горад Кенігсберг (зараз ён называецца Калінінград) стаіць на рацэ. Некалі там было 7 мастоў, якія звязвалі паміж сабой берагі і два астраўкі. Жыхары горада заўважылі, што яны ніяк не могуць здзейсніць прагулку па ўсіх сямі мастах, прайшоўшы па кожнаму з іх роўна адзін раз. 

Так з’явілася галаваломка: "Ці можна прайсці ўсе сем кёнігсбергскіх мастоў роўна адзін раз і вярнуцца ў зыходнае месца?". 

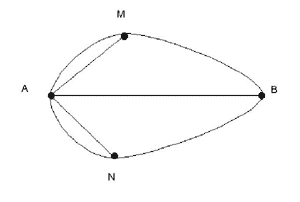
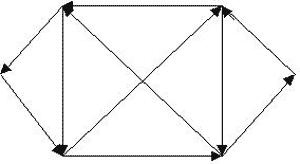
У 1735 годзе гэта задача стала вядомая Леанарду Эйлеру. Эйлер высветліў, што такога шляху няма, г. зн. даказаў, што гэтая задача невырашальная. Вядома, Эйлер рашыў не толькі задачу аб кёнігсбергскіх мастах, а цэлы клас аналагічных задач, для якіх распрацаваў метад рашэння. Можна заўважыць, што задача складаецца ў тым, каб па карце правесці маршрут - лінію, не адрываючы алоўка ад паперы, абыйсці ўсе сем мастоў і вярнуцца ў пачатковую кропку. Таму Эйлер стаў разглядаць замест карты мастоў схему з пунктаў і ліній, адкінуўшы масты, узгоркі і берагі, як нематэматычныя паняцці. Вось што ў яго атрымалася:

А, В - узгоркі, M, N - берагі, а сем крывых - сем мастоў. 

Зараз задача такая - абысці контур на малюнку так, каб кожная крывая праводзілася роўна адзін раз. У наш час такія схемы з пунктаў і ліній сталі называць графамі, пункты называюць вяршынямі графа, а лініі - рэбрамі графа. У кожнай вяршыні графа сыходзіцца некалькі ліній. Калі лік ліній цотны, то вяршыня называецца цотнай, калі лік вяршынь няцотны, то вяршыня называецца няцотнай. 

Дакажам невырашальнасць нашай задачы. Як бачым, у нашым графе ўсе вяршыні няцотныя. Для пачатку дакажам, што, калі абыход графа пачынаецца не з няцотнага пункту, то ён абавязкова павінен скончыцца ў гэтым пункце.

Разгледзім для прыкладу вяршыню з трыма лініямі. Калі мы па адной лініі прыйшлі, па іншай выйшлі, і па трэцяй зноў вярнуліся. Усё, далей ісці няма куды (рэбраў больш няма). У нашай задачы мы сказалі, што ўсе пункты няцотныя, значыць, выйшаўшы з адной з іх, мы павінны скончыць адразу ў трох астатніх няцотных пунктах, чаго не можа быць. Да Эйлера ні каму ў галаву не прыходзіла, што галаваломкі аб мастах і іншыя галаваломкі з абыходам контуру, мае дачыненне да матэматыкі. Аналіз Эйлера такіх задач "з'яўляецца першым парасткам новай вобласці матэматыкі, сёння вядомай пад назвай тапалогія". 

Тапалогія - гэта раздзел матэматыкі, які вывучае такія ўласцівасці фігур, якія не мяняюцца пры дэфармацыях, якія вырабляюцца без парываў і склейвання. Напрыклад, з пункту гледжання тапалогіі, круг, эліпс, квадрат і трохвугольнік валодаюць аднолькавымі ўласцівасцямі і з'яўляюцца адной і той жа фігурай, так як могуць дэфармавацца адну ў іншую, а вось кольца да іх не ставіцца, бо, каб яго дэфармаваць у круг, неабходнае злепліванне. 

Правілы  вычэрчвання графа. 

1. Калi ў графе няма няцотных пунктаў, то яго можна начарціць адным росчыркам, не адрываючы алоўка ад паперы, пачынаючы з любога месца. 

2. Калi ў графе дзве няцотныя вяршыні, то яго можна начарціць адным росчыркам, не адрываючы алоўка ад паперы, прычым вычэрчванне трэба пачынаць у адной няцотнай кропцы, а скончыць у іншай.

 3. Калi ў графе больш за два няцотныя пункты, то яго нельга начарціць адным росчыркам алоўка. 

Вернемся да нашай задачы з адкрытым канвертам. Падлічым колькасць цотных і няцотных кропак: 2 няцотныя і 3 цотныя, значыць, гэтую фігуру можна начарціць адным росчыркам, прычым пачаць трэба ў няцотнай кропцы. 

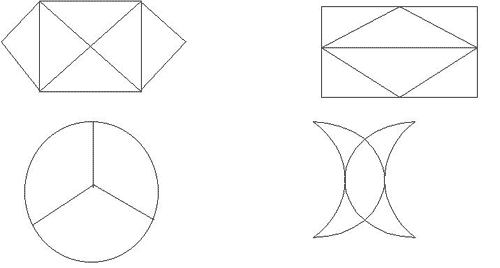
Вызначце, якія фігуры можна пабудаваць, а якія нельга. 

а) Усе пункты цотныя, таму гэтую фігуру можна пабудаваць, пачынаючы з любога месца, напрыклад:

б) У гэтай фігуры два няцотныя пункты, таму яе можна пабудаваць не адрываючы, алоўка ад паперы, пачынаючы з няцотнага пункта. 

в) У гэтай фігуры чатыры няцотныя пункты, таму яе нельга пабудаваць.

 г) Тут усе пункты цотныя, таму яе можна пабудаваць, пачынаючы з любога месца. 

Праверце, ці можна здзейсніць прагулку па ўсіх мастах, прайшоўшы па кожнаму з іх роўна адзін раз. І калі можна, то намаляваць шлях.

32.Задачы на разразанне

Задачамі на разразанне навукоўцы займаліся з самых старажытных часоў. Першы сістэматычны трактат належыць Абул-Вэфа, знакамітаму персіцкаму астраному X стагоддзя, які жыў у Багдадзе.

 

Пазней вучоныя заняліся рашэннем задач на разразанне      фігур, на найменшы лік частак, і наступнае складанне з іх новай фігуры толькі ў XX ст.  Тады гэтым займаўся Генры Э. Дзьюдзені.

Займальныя задачы на разразанне фігур - частак. 

 Адна з самых вядомых старажытных геаметрычных галаваломак - гульня ТАНГРАМ. Зарадзілася  гульня ў Кітаі, дзе яна называецца «чы чао тую», гэта значыць «мудрагелісты ўзор з сямі частак». На працягу вось ужо некалькіх тысячагоддзяў гэтая гульня служыць любімай забавай у краінах Усходу, а з пачатку XIX стагоддзя яна атрымала распаўсюджванне і на Захадзе. Расказваюць, што Напалеон, знаходзячыся ў выгнанні на востраве Святой Алены гадзінамі займаўся складаннем малюнкаў з элементаў ТАНГРАМА.

Назва «танграм» - еўрапейская. Верагодней за ўсё, яна утварылася ад слова «тань» (што азначае «кітаец») і кораня «грама» (у перакладзе з грэцкага «лінія»).

 Пра гульню ТАНГРАМ існуе такая легенда:  Гэта было вельмі даўно, амаль дзве з паловай тысячы гадоў таму назад. У немаладога імператара Кітая нарадзіўся доўгачаканы сын і наследнік. Ішлі гады. Хлопчык рос здаровым і кемлівым не па гадах. Адно турбавала старога імператара: яго сын, будучы ўладар велізарнай краіны, не хацеў вучыцца. Хлопчыку давала вялікае задавальненне цэлы дзень бавіцца цацкамі. Імператар заклікаў да сябе трох мудрацоў, адзін з якіх быў вядомы як матэматык, другі праславіўся як мастак, а трэці быў знакамітым філосафам, і загадаў ім прыдумаць гульню, забаўляючыся якой, яго сын спасціг бы пачаткі матэматыкі, навучыўся глядзець на навакольны свет пільнымі вачыма мастака , стаў бы цярплівым, як праўдзівы філосаф, і зразумеў бы, што часта складаныя рэчы складаюцца з простых рэчаў. І тры мудрацы прыдумалі гэтую гульню. На першы погляд, гульня вельмі простая. Усё, што патрабуецца - гэта скласці з дэталяў (яны атрымліваюцца разразаннем квадрата на сем частак) якую-небудзь постаць. Аднак, задача толькі здаецца лёгкай. Не ўсякі дарослы зможа скласці самыя мудрагелістыя камбінацыі фігурак ТАНГРАМА.

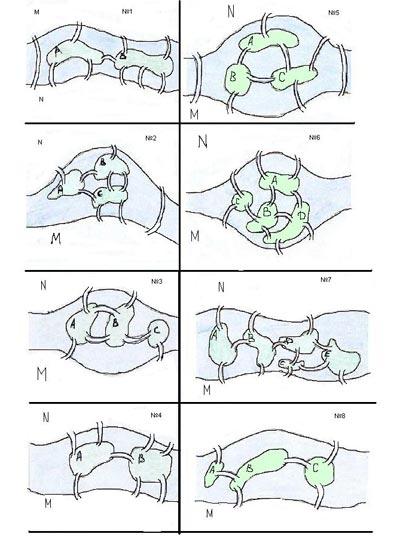
Танграм складаецца з 7 плоскіх геаметрычных фігур - ТАНАЎ. Будзем называць іх так: два вялікія роўныя трохвугольнікі, два маленькія роўныя трохвугольнікі, адзін сярэдні трохвугольнік, адзін квадрат, адзін паралелаграм (для прастаты будзем называць яго чатырохвугольнікам).Зыходная фігура - вялікі квадрат. 

Галаваломка складаецца ў тым, што трэба выкарыстоўваючы ўсе сем частак, скласці фігуркі, прапанаваныя на малюнку (або скласці фігуркі самім). Фігуры павінны прымыкаць адна да адной, не накладваючыся пры гэтым.

33.Мнагаграннікі

Мнагаграннікам называецца цела, мяжа якога з'яўляецца аб'яднаннем канчатковага ліку многавугольнікаў. Першыя згадкі пра мнагаграннік вядомыя яшчэ за тры тысячы гадоў да нашай эры ў Егіпце і Вавілоне. Але тэорыя мнагаграннікаў з'яўляецца і сучасным раздзелам матэматыкі. Яна цесна звязана з тапалогіяй, тэорыяй графаў, мае вялікае значэнне як для тэарэтычных даследаванняў па геаметрыі, так і для практычнага прымянення ў іншых раздзелах матэматыкі, напрыклад, у алгебры, тэорыі лікаў, прыкладной матэматыцы - лінейным праграміраванні. Мнагаграннікі маюць прыгожыя формы, напрыклад, правільныя, паўправільныя і зорчатыя мнагаграннікі. Яны валодаюць багатай гісторыяй, якая звязана з імёнамі такіх вучоных, як Піфагор, Еўклід, Архімед. Са старажытных часоў нашы ўяўленні аб прыгажосці звязаны з сіметрыяй. Напэўна, гэтым тлумачыцца цікавасць чалавека да мнагаграннікаў - дзіўным сімвалам сіметрыі, якія прывабліваюць увагу выдатных мысліцелей. 

Гісторыя правільных мнагаграннікаў сыходзіць у глыбокую старажытнасць. Правільныя мнагаграннікі вывучалі  Піфагор і яго вучні. Іх ўражвала прыгажосць, дасканаласць, гармонія гэтых фігур. 

Піфагарыйцы лічылі правільныя мнагаграннікі чароўнымі фігурамі і выкарыстоўвалі ў сваіх філасофскіх працах: першаасновам быцця - агню, зямлі, паветру, вадзе надавалася форма адпаведнага мнагагранніка: тэтраэдра, куба, актаэдра, ікасаэдра, а ўвесь Сусвет меў форму дадэкаэдра. 

Пазней вучэнне піфагарэйцаў аб правільных мнагагранніках выклаў у сваіх працах іншы старажытнагрэчаскі вучоны, філосаф - ідэаліст Платон. З тых часоў правільныя мнагаграннікі сталі называцца Платонавымі целамі. 

Існуе пяць тыпаў правільных мнагаграннікаў: тэтраэдр, гексаэдр (куб), актаэдр, дадэкаэдр, ікасаэдр.Чаму правільныя мнагаграннікі атрымалі такія імёны? Гэта звязана з лікам іх граней. Тэтраэдр мае 4 грані, у перакладзе з грэчаскага "тэтра" - чатыры, "эдрон" - грань. гексаэдр (куб) мае 6 граней, "гекса" - шэсць; актаэдр - васьміграннік, "актоіх" - восем; дадэкаэдр - дванаццаціграннік, "дадека" - дванаццаць; ікасаэдр мае 20 граней, "ікас" - дваццаць. 

Першыя згадкі пра мнагаграннік вядомыя яшчэ за тры тысячы гадоў да нашай эры ў Егіпце і Вавілоне. Дастаткова ўспомніць знакамітыя егіпецкія піраміды і самую вядомую з іх - піраміду Хеопса. Гэта правільная піраміда, у аснове якой квадрат са стараной 233 м і вышыня якой дасягае 146,5 м. Не выпадкова кажуць, што піраміда Хеопса - нямы трактат па геаметрыі. Гісторыя правільных мнагаграннікаў сыходзіць у глыбокую старажытнасць. Пачынаючы з 7 стагоддзя да нашай эры ў Старажытнай Грэцыі ствараюцца філасофскія школы. Вялікае значэнне ў гэтых школах набываюць развагі, з дапамогай якіх удалося атрымліваць новыя геаметрычныя ўласцівасці. Адной з першых і самых вядомых школ была школа Піфагора, названая ў гонар свайго заснавальніка Піфагора. Адметным знакам піфагарэйцаў была пентаграма, на мове матэматыкі - гэта правільны нявыпуклы або зорчаты пяцiвугольнiк. Пентаграме прысвойвалася здольнасць абараняць чалавека ад злых духаў.

Мнагаграннікі ў прыродзе  Правільныя мнагаграннікі - самыя выгадныя фігуры, таму яны шырока распаўсюджаныя ў прыродзе. Пацвярджэннем таму служыць форма некаторых крышталяў. Напрыклад, крышталі паваранай солі маюць форму куба. Пры вытворчасці алюмінія выкарыстоўваецца алюмініева-каліевы кварц, монакрышталі якога маюць форму правільнага актаэдра. Атрыманне сернай кіслаты, жалеза, асаблівых гатункаў цэменту не абыходзіцца без сярністага калчадана. Крышталі гэтага хімічнага рэчыва маюць форму дадэкаэдра. У розных хімічных рэакцыях ужываецца сурменісты сернакіслы натрый - рэчыва, сінтэзаванае вучонымі. Яго крышталь мае форму тэтраэдра. Яшчэ адзін правільны мнагаграннік - ікасаэдр перадае форму крышталяў бору. 

Алмаз (актаэдр)

Шэеліт (піраміда)

Хрусталь (прызма)

Павараная соль (куб)

Правільныя мнагаграннікі сустракаюцца гэтак жа і ў жывой прыродзе. Напрыклад, шкілет аднаклетачнага арганізма феадарыі (Circjgjnia icosahtdra) па форме нагадвае ікасаэдр.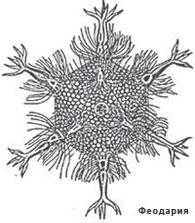

 Большасць феадарый жывуць на марской глыбіні і служаць здабычай каралавых рыбак. Але найпрасцейшая жывёла абараняе сябе дванаццаццю іголкамі, якія выходзяць з 12 вяршыняў шкілета. Яно больш падобна на звёздчаты мнагаграннік. З усіх мнагаграннікаў з тым жа лікам граняў ікасаэдр мае найбольшы аб'ём пры найменшай плошчы паверхні. Гэта ўласцівасць дапамагае марскому арганізму пераадольваць ціск тоўшчы вады.

34.Прасцейшыя задачы прыкладнога характару

Перад чалавекам да розуму, як казаў старажытны мысліцель і філосаф Канфуцый, які жыў прыкладна 2,5 тысячы гадоў таму,  тры шляхі:

шлях разважання - гэта шлях самы высакародны,

шлях пераймання - гэта шлях самы лёгкі і

шлях вопыту - гэта шлях самы горкі. 

Нягледзячы на ​​тое, што шлях вопыту - самы горкі, ужо за некалькі стагоддзяў да нашай эры ў Вавілоне, Кітаі і Грэцыі існавалі пачатковыя геаметрычныя веды, якія здабываліся дасведчаным шляхам. 

Геаметрыя - адна з самых старажытных навук. У перакладзе з грэчаскага слова «геаметрыя» азначае «землямер» ( «гео» - зямля, «метрео» - мераць). Такая назва тлумачыцца тым, што зараджэнне геаметрыі было звязана з рознымі вымяральнымі працамі, якія даводзілася выконваць пры разметцы зямельных участкаў, правядзенні дарог, будаўніцтве будынкаў і іншых збудаванняў. У выніку гэтай дзейнасці з'явіліся і паступова назапашваліся розныя правілы, звязаныя з геаметрычнымі вымярэннямі і пабудовамі. Такім чынам, геаметрыя ўзнікла на аснове практычнай дзейнасці людзей і ў пачатку свайго развіцця служыла пераважна практычным мэтам. 

Вялікія матэматыкі таго часу - Фалес, Піфагор, Архімед, Платон, Еўклід унеслі вялікі ўклад у яе развіццё. Ужо ў старажытным свеце людзі займаліся рашэннем практычных задач. Зыходзячы з практыкі, паўстала і тэорыя. 

Рашэнне практычных задач старажытнымі геаметрамі дазваляе:

• знаходзіць на мясцовасці адлегласць паміж двума пунктамі, якое немагчыма прайсці па прамой; 

• знаходзіць на мясцовасці адлегласць паміж двума пунктамі, адзін з якіх недаступны;

 • вызначаць вышыню высокіх прадметаў; 

• будаваць прамыя вуглы на мясцовасці;

 • знаходзіць даўжыню вялікай акружнасці;

 • вызначаць без компаса бакі гарызонту; 

• будаваць акружнасць пры дапамозе вяроўкі і г.д. 

Гістарычныя звесткі. 

Землямеры  Старажытнага Егіпта для пабудовы прамога вугла карысталіся наступным прыёмам. Вяроўку вузламі дзялілі на 12 роўных частак і канцы звязвалі. Затым вяроўку расцягвалі на зямлі так, што атрымліваўся трохвугольнік з бакамі 3, 4 і 5 дзяленняў. Вугал трохвугольніка, процілеглы баку ў 5 дзяленняў, быў прамы. Калі рамеснікі карысталіся вяроўкай заўсёды адной і той жа строга вызначанай даўжыні, то плошча такога прамавугольнага трохвугольніка прымалася за эталон. У цяперашні час такі трохвугольнік называецца «егіпецкі» у гонар краіны, у якой быў «адкрыты». 

У старажытныя часы егіпцяне, прыступаючы да пабудовы піраміды, палаца або звычайнага дома, спачатку адзначалі кірунак бакоў гарызонту. Гэта вельмі важна, так як асветленасць ў будынку залежыць ад становішча яго вокнаў і дзвярэй у адносінах да сонца. Дзейнічалі яны наступным чынам. Утыкалі ў зямлю стромы шост. У апоўдні цень ад шаста станавілася карацей за ўсё і паказвала накірунак на поўнач. Егіпецкія будаўнікі намячалі лінію поўнач - поўдзень. Для правядзення лініі ўсход - захад бралі вяроўку з двума калкамі і праводзілі на зямлі дугі так, як гэта паказана на малюнку. 

Праз пункты перасячэння дуг нацягвалі вяроўку. Гэта і ёсць накірунак з усходу на захад.

 Егіпцяне таксама ўмелі знаходзіць даўжыню акружнасці. У глыбокай старажытнасці лічылася, што для гэтага дастаткова ўзяць самую шырокую частку сярэдзіннага перасеку бочкі і памножыць яе на 3. Гэта было не строга дакладна, але цалкам дастаткова для штодзённых вымярэнняў. 

Аднойчы грэчаскаму вучонаму Фалесу прапанавалі знайсці вышыню велічэзнай піраміды. Ён уваткнуў доўгую палку вертыкальна ў зямлю і сказаў: «Калі цень ад гэтай палкі будзе той жа даўжыні, што і сама палка, цень ад піраміды будзе мець тую ж даўжыню, што і вышыня піраміды». 

Фалес умеў знаходзіць адлегласць да недаступных пунктаў, ужываючы прыкметы роўнасці і падабенства трохвугольнікаў. Ён даказаў, што дыяметр дзеліць круг напалову, што пры згінанні круга па дыяметры адна палова ў дакладнасці ляжа на іншую. 

Ён таксама ведаў, што ўтвораныя пры перасячэнні дзвюх прамых вертыкальныя вуглы роўныя. 

Жыхарамі краін Старажытнага Свету шырока выкарыстоўваліся веды па геаметрыі. Пра гэта сведчаць папірусы, знойдзеныя ў схованках гэтых краін. Мяркуючы па захаваўшымся задачах, матэматыкам Вавілона было ўжо вядома ўласцівасць сярэдняй лініі трапецыі. У кнігах старажытнаіндыйскай геаметрыі сустракаюцца апісанні вылічэнні плошчаў, пабудовы квадрата па дадзенай яго старане, дзяленне адрэзка напалову.

Кітайскім вучоным было вядома правіла для вызначэння плошчы круга: «Памножым дыяметр сам на сябе, раздзялі на 4, вазьмі тры разы». 

Вымярэнні голымі рукамі. «Змерай самога сябе - і ты станеш сапраўдным геаметрам!" - усклікнуў сярэднявечны філосаф Марсілія Фічына. Вядома, вымераць самога сябе і стаць сапраўдным геаметрам вельмі цяжка. Не кожнаму ўдаецца зрабіць гэта за ўсё жыццё. Кожнаму чалавеку, які навучыўся лічыць і пісаць, неаднаразова даводзілася што-небудзь вымяраць: вышыню дрэва, уласную вагу, даўжыню скачка і многае іншае. Але не заўсёды ў падарожжы мы маем сантыметровую стужку. Добра было б кожнаму з нас абзавесціся «жывым метрам», каб у выпадку патрэбы карыстацца ім для вымярэнняў. Карысна таксама памятаць, што ў большасці людзей адлегласць паміж канцамі расстаўленых рук роўна росту - правіла, прыкмечанае геніяльным мастаком і навукоўцам Леанарда да Вінчы: яно дазваляе карыстацца нашымі «жывымі метрамі». 

Мастацтва мераць крокамі. Апынуўшыся на дарозе, мы можам выканаць шэраг цікавых геаметрычных вымярэнняў. Перш за ўсё, выкарыстаем шашу, каб вымераць даўжыню свайго кроку і хуткасць хады. Гэта дасць магчымасць вымяраць адлегласці крокамі - навык, які набываецца даволі лёгка пасля нядоўгіх практыкаванняў. Галоўнае тут- прывучыць сябе рабіць крокі заўсёды аднолькавай даўжыні. На шашы праз кожныя 100 м усталяваны белы слуп, прайшоўшы такі 100-метровы прамежак сваім звычайным крокам і злічыўшы лік крокаў, вы лёгка знойдзеце сярэднюю даўжыню свайго кроку. 

Адзначым цікавыя суадносіны, выяўленыя шматразовымі вымярэннямі: сярэдняя даўжыня кроку дарослага чалавека роўная прыкладна палове яго росту, лічачы да ўзроўню вачэй. Калі, напрыклад, рост чалавека да ўзроўню вачэй 1,4 м, то даўжыня яго кроку - каля 70 см.

Як вызначыць вышыню высокага прадмета спосабам Жуля Верна

Узяць шост, вымераць яго даўжыню і вертыкальна ўторкнуць у зямлю насупраць высокага прадмета, вышыню якога трэба знайсці. Другому ўдзельніку трэба легчы на ​​зямлю так, каб край шаста супаў з самай высокай кропкай прадмета. Адлегласць ад шаста да галавы ўдзельніка так адносіцца да адлегласці ад галавы да асновы высокага прадмета, як вышыня шаста да вышыні прадмета. Застаецца вылічыць вышыню прадмета так: вышыню шаста памножыць на адлегласць ад прадмета да галавы ўдзельніка, які ляжыць на зямлі, і падзяліць на адлегласць ад шаста да галавы ўдзельніка.

Як вызначыць бакі гарызонту

Егіпецкія будаўнікі рабілі так. Утыкалі ў зямлю стромы шост. У поўдзень, калі цень ад шаста была карацей за ўсё, яна паказвала кірунак на поўнач. Азначаецца на зямлі лінія поўнач-поўдзень.Затым бярэцца вяроўка з двума калкамі і праводзяцца на зямлі дугі так, як гэта паказана на малюнку. 

Праз кропкі перасячэння дуг нацягваецца вяроўка. Гэта і будзе напрамак з усходу на захад. Дарэчы, лініі поўнач-поўдзень і захад-ўсход перасякаюцца пад прамым вуглом. Таму, можна з планак вырабіць прамавугольны трохвугольнік і выкарыстоўваць яго ў выпадку неабходнасці. 

Як вымяраць голымі рукамі

Калісьці геніяльны мастак і навуковец Леанарда да Вінчы прымеціў правіла, што ў большасці людзей адлегласць паміж канцамі расстаўленых рук роўна росту чалавека. Але спадзявацца на сярэднюю велічыню не варта: кожны павінен вымераць свой рост і размах сваіх рук. 

Задачы знаходжання адлегласцей да недаступных пунктаў у старажытнасці вырашаў Фалес. У наш час рашэнне такіх задач таксама знаходзіць прымяненне. Выкарыстоўваючы прыкметы падабенства трохвугольнікаў, можна знаходзіць на мясцовасці адлегласць паміж двума пунктамі, якое немагчыма прайсці па прамой лініі і адлегласць паміж двума пунктамі, адзін з якіх недаступны. Абедзве задачы сустракаюцца ў падручніку А.В.Пагарэлава. З мноства існуючых спосабаў вымярэння вышыні дрэва, не ссякаючы яго і не ўзбіраючыся на верхавіну, пры дапамозе вельмі немудрагелістых прыбораў і нават без усялякіх прыстасаванняў можна выбраць самы лёгкі і самы старажытны спосаб - той, якім грэчаскі мудрэц Фалес за шэсць стагоддзяў да нашай эры вызначыў у Егіпце вышыню піраміды. Ён выкарыстаў яе цень. Фалес, - кажа паданне, - выбраў дзень і час, калі даўжыня ўласнай яго цені была роўная яго росту.  У гэты момант вышыня піраміды павінна таксама раўняцца даўжыні сваёй цені. А каб выкарыстаць цень для вырашэння задачы аб вышыні піраміды, трэба было валодаць ведамі аб некаторых геаметрычных ўласцівасцях трохвугольніка. Спосаб Фалеса ў паказаным выглядзе не заўсёды дакладны, так як сонца ў нас нізка стаіць над гарызонтам, і цені роўныя вышыні прадметаў бываюць толькі ў поўдзень у часы летніх месяцаў. Няцяжка, аднак, змяніць гэты спосаб так, каб у сонечны дзень можна было карыстацца любым ценем, якой бы даўжыні ён ні быў. Вымераўшы, акрамя таго, і свой цень ці цень якога-небудзь шаста, вылічваюць шуканую вышыню з прапорцыі: AB: А1В1 = BC: В1С1 г.зн. вышыня дрэва ў гэтулькі жа разоў больш вашай уласнай вышыні, у колькі разоў цень дрэва даўжэй вашага ценю.

35. Задачы і галаваломкі з запалкамі

1. Дакладная роўнасць

Заданне. Трэба перамясціць толькі адну запалку ў выкладзеным запалкамі арыфметычным прыкладзе «8 + 3 - 4 = 0» так, каб атрымалася правільная роўнасць (можна змяняць і знакі, лічбы). 

2. Развярнуць рыбку

Заданне. Перастаўце тры запалкі так, каб рыбка паплыла ў зваротным кірунку. Іншымі словамі, трэба павярнуць рыбу на 180 градусаў па гарызанталі. 

.

Адказы:

1		2

3		4

		6
5

7		8