Краіна звычайных дробаў

16. Гісторыя ўзнікнення звычайных дробаў. 

Неабходнасць у выкарыстанні дробавых лікаў паўстала ў чалавека на вельмі ранняй стадыі развіцця. Ужо дзяльба здабычы, якая складалася з некалькіх забітых жывёл, паміж удзельнікамі палявання, калі лік жывёл аказваўся не кратным ліку паляўнічых, магла прывесці першабытнага чалавека да паняцця аб дробавым ліку. 

Адначасова з неабходнасцю лічыць прадметы ў людзей са старажытных часоў з'явілася патрэба вымяраць даўжыню, плошчу, аб'ём, час і іншыя велічыні. Вынік вымярэнняў не заўсёды атрымоўвалася паказаць натуральным лікам, даводзілася ўлічваць і часткі меры. 

Гістарычна дробы ўзніклі ў працэсе вымярэння. Патрэба ў больш дакладных вымярэннях прывяла да таго, што пачатковыя адзінкі меры пачалі драбніць на 2, 3 і больш частак. Больш дробнай адзінцы меры, якую атрымлівалі як вынік раздрабнення, давалі індывідуальную назву, і велічыні вымяралі ўжо гэтай больш дробнай адзінкай. 

У сувязі з гэтай неабходнай працай людзі пачалі шукаць выразы: палова, трэць, два з паловай кроку. Адкуль можна было зрабіць выснову, што дробавыя лікі паўсталі як вынік вымярэння велічынь. 

Народы прайшлі праз многія варыянты запісу дробаў, пакуль не прыйшлі да сучаснага запісу. 

Дробы ў Старажытным Егіпце

У Старажытным  Егіпце  архітэктура дасягнула высокага  развіцця. Для таго, каб будаваць грандыёзныя піраміды і храмы, каб вылічваць даўжыні, плошчы і аб'ёмы фігур, неабходна было ведаць арыфметыку. З расшыфраваных звестак на папірусе вучоныя даведаліся, што егіпцяне 4 000 гадоў таму мелі дзесятковую (але не пазіцыйную) сістэму злічэння, умелі рашаць многія задачы, звязаныя з патрэбамі будаўніцтва, гандлю і ваеннай справы. У Старажытным Егіпце некаторыя дробы мелі свае асаблівыя назвы - а менавіта, часта ўзнікаючыя на практыцы 1/2, 1/3, 2/3, 1/4, 3/4, 1/6 і 1/8. Акрамя таго, егіпцяне ўмелі аперыраваць з так званымі аліквотнымі дробамі, (ад лац. Aliquot - некалькі) тыпу 1/n - іх таму часам таксама называюць «егіпецкімі»; гэтыя дробы мелі сваё напісанне: выцягнуты гарызантальны авальчык і пад ім пазначэнне назоўніка. Адным з першых вядомых згадак аб егіпецкіх дробах з'яўляецца матэматычны папірус Рында. Тры найбольш старажытныя тэксты, у якіх згадваюцца егіпецкія дробы - гэта Егіпецкі матэматычны скураны скрутак, Маскоўскі матэматычны папірус і Драўляная таблічка Ахміма. Папірус Рында ўключае табліцу егіпецкіх дробаў для рацыянальных лікаў выгляду 2/n, а таксама 84 матэматычныя задачы, іх рашэнні і адказы, запісаныя ў выглядзе егіпецкіх дробаў. 

Егіпцяне ставілі іерогліф над лікам для абазначэння адзінкавага дробу ў звычайным запісе, а ў святых тэкстах выкарыстоўвалі лінію. Да прыкладу:

У іх таксама былі адмысловыя знакі для дробаў 1/2, 2/3 і 3/4, якімі можна было запісваць таксама іншыя дробы (большыя чым 1/2).

 Астатнія дробы яны запісвалі ў выглядзе сумы доляў. Дроб яны запісвалі ў выглядзе сумы, але знак «+» не паказвалі. Такі запіс змешаных лікаў (без знака «+») захаваўся з тых часоў. 

Старажытныя егіпцяне ўжо ведалі, як падзяліць 2 прадметы на траіх, для гэтага ліку - 2/3 - у іх быў спецыяльны значок. Гэта быў адзіны дроб ва ўжытку егіпецкіх пісцоў, у якім у лічніку не стаяла адзінка - усе астатнія дробы абавязкова мелі ў лічніку адзінку (так званыя асноўныя дробы). Умелі егіпцяне таксама перамнажаць і дзяліць дробы. Але для множання даводзілася перамнажаць долі на долі, а потым, магчыма, зноў выкарыстоўваць табліцу. Яшчэ складаней ішла справа з дзяленнем. 

Вялікую работу па даследаванні егіпецкіх дробаў правёў матэматык XIII стагоддзя Фібаначы. 

Малюнак дробаў у Старажытным Егіпце

Дроб у Старажытнай Грэцыі. Паколькі грэкі працавалі са звычайнымі дробамі толькі эпізадычна, яны выкарыстоўвалі розныя абазначэнні.

Герон і Дыяфант, самыя вядомыя арыфметыкі сярод старажытнагрэчаскіх матэматыкаў, запісвалі дробы ў алфавітнай форме, прычым лічнік размяшчалі пад назоўнікам.   Недахопы грэчаскай сістэмы злічэння можна аднесці хучэй за кошт іх зацятага імкнення да строгасці, якое прыкметна павялічыла цяжкасці, звязаныя з аналізам адносіны несувымерных велічынь. Слова «лік» грэкі разумелі як набор адзінак, таму тое, што мы цяпер разглядаем як адзіны рацыянальны лік - дроб, - грэкі разумелі як стаўленне двух цэлых лікаў. Менавіта гэтым тлумачыцца, чаму звычайныя дробы рэдка сустракаліся ў грэчаскіх заданнях. 

Максім Плануд грэчаскі манах, вучоны, матэматык ў 13 стагоддзі ўвёў назву лічнік і назоўнік.  

У Грэцыі ўжываліся разам з адзінкавымі, «егіпецкімі» дробамі і агульныя звычайныя дробы. Сярод розных запісаў ўжывалася і такая: зверху назоўнік, пад ім - лічнік дробу. Напрыклад, 5/3 азначала тры пятых. Яшчэ за 2-3 стагоддзі да Еўкліда і Архімеда грэкі свабодна валодалі арыфметычнымі дзеяннямі з дробамі. 

Малюнак дробаў ў Старажытнай Грэцыі

Дробы ў Індыі. Сучасную сістэму запісу дробаў стварылі ў Індыі. Толькі там пісалі назоўнік зверху, а лічнік знізу, і не пісалі дробавай рысы. Затое ўвесь дроб змяшчаўся ў прамавугольную рамку. Часам выкарыстоўваўся і «трохпавярховы» выраз з трыма лікамі ў адной рамцы; у залежнасці ад кантэксту гэта магло абазначаць няправільную дроб (a + b / c) або дзяленне цэлага ліку a на дроб b / c. Правілы дзеянняў над дробамі амаль не адрозніваліся ад сучасных. У індыйскагага матэматыка Брахмагупты мы знаходзім дастаткова развітую сістэму дробаў. У яго сустракаюцца розныя дробы: і асноўныя, і з любым лічнікам.

Дробы ў арабаў. Запісваць дроб як цяпер, сталі арабы. Сярэднявечныя арабы карысталіся трыма сістэмамі запісу дробаў. 

Па-першае, на індыйскі манер запісвалі назоўнік пад лічнік, дробавая рыса з'явілася ў канцы XII - пачатку XIII ст.

Па-другое, чыноўнікі, каморнікі, гандляры карысталіся вылічэннем аліквотных дробаў, падобным на егіпецкія, пры гэтым ужываліся дробы  з назоўнікам, які не перавышае10 (толькі для такіх дробаў арабская мова мае адмысловыя тэрміны), часта выкарыстоўваліся набліжаныя значэнні. 

Па-трэцяе, арабскія вучоныя атрымалі ў спадчыну вавілонска-грэчаскую шасцідзесяцярычную сістэму, у якой, як і грэкі, ужывалі алфавітны запіс, распаўсюджваючы яго і на цэлыя часткі. 

Малюнак дробаў у арабаў

Дробы ў Вавілоне

Вавіланяне карысталіся усяго двума лічбамі. Вертыкальная рысачка пазначала адну адзінку, а вугал з двух ляжачых рысачак - дзесяць. Гэтыя рысачкі ў іх атрымліваліся ў выглядзе клінаў, таму што вавіланяне пісалі вострай палачкай на сырых гліняных дошчачках, якія потым сушылі і абпальвалі. У старажытным Вавілоне аддавалі перавагу пастаяннаму назоўніку, роўнаму 60-ці. Шасцідзесяцярычнымі дробамі, запазычанымі ад Вавілона, карысталіся грэчаскія і арабскія матэматыкі і астраномы. 

Даследчыкі па-рознаму тлумачаць з'яўленне ў вавіланян шасцідзесяцярычнай сістэмы злічэння. Хутчэй за ўсё тут улічвалася асаблівасць  ліку 60, які кратны 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 і 60, што значна палягчае ўсякія разлікі. Вавілонская матэматыка аказала ўплыў на грэчаскую матэматыку. Сляды вавілонскай шасцідзесяцярычнай сістэмы злічэння ўтрымліваюцца ў сучаснай навуцы пры вымярэнні часу і градуснай меры вуглоў. Да нашых дзён захавалася дзяленне гадзіны на 60 мін., хвіліны на 60 с, акружнасці на 360 градусаў, градуса на 60 мін.

Малюнак дробаў ў Старажытным Вавілоне

17. Лікі – ліліпуты

Мы падарожнічаем у зваротным парадку: пазнаёміўшыся з лікавымі волатамі, пераходзім да ліліпутаў, - да лікаў, якія ў гэтулькі ж разоў меншыя за 1, у колькі разоў адзінка менш лікавага велікана. Адшукаць прадстаўнікоў гэтага свету не складае ніякай цяжкасці: для гэтага дастаткова напісаць рад лікаў, адваротных мільёну, мільярду і т. д., г. зн. дзяліць 1 на гэтыя лікі. 

Атрыманыя дробы ёсць тыповыя лікавыя ліліпуты, такія ж пігмеі ў параўнанні з адзінкай, якім з'яўляецца адзінка ў параўнанні з мільёнам, мільярдам, мільёнамі і іншымі лікавымі веліканамі. Вы бачыце, што кожнаму ліку-велікану адпавядае лік-ліліпут, і што, такім чынам, лікавых ліліпутаў існуе не менш, чым веліканаў. Для іх таксама прыдуманы скарочаны спосаб абазначэння. Мы ўжо згадвалі, што вельмі вялікія лікі  ў навуковых працах (па астраноміі, фізіцы) абазначаюцца так:

Адпаведна гэтаму, лікавыя ліліпуты абазначаюцца наступным чынам:

Ці ёсць, аднак, рэальная патрэба ў падобных дробах?  Ці прыходзіцца калі-небудзь сапраўды мець справу з такімі дробнымі долямі адзінкі? Пра гэта цікава пагутарыць падрабязней. 

Ліліпуты часу

Секунда, па звычайным прадстаўленні, ёсць настолькі малы прамежак часу, што з вельмі дробнымі часткамі яе не прыходзіцца мець справы ні пры якіх абставінах. Лёгка напісаць - 1/1000 секунды, - але гэта чыста папяровая велічыня, таму што нічога не можа адбыцца ў такі мізэрны прамежак часу. Так думаюць многія, - але памыляюцца, таму што ў тысячную долю секунды могуць паспець стацца вельмі розныя з'явы. Цягнік, які праходзіць 36 кіламетраў у гадзіну, робіць у секунду 10 метраў, і, такім чынам, на працягу 1000-ай долі секунды паспявае прасунуцца на адзін сантыметр. Гук у паветры пераносіцца на працягу 1000-ай долі секунды на 33 сантыметры, а куля, якая пакідае ружэйны ствол з хуткасцю 700-800 метраў у секунду, пераносіцца за той жа прамежак часу на 70 сантыметраў. Зямны шар перамяшчаецца кожную 1000-ую долю секунды, у сваім звароце вакол сонца, на 30 метраў. Струна, якая выдае высокі тон, робіць у 1000-ю долю секунды 2-4 і больш поўных ваганняў; нават камар паспявае ў гэты час узмахнуць уверх ці ўніз сваімі крылцамі. Маланка доўжыцца значна менш 1000-ай долі секунды: на працягу гэтага прамежку часу паспявае паўстаць і спыніцца такая грозная з'ява прыроды (маланка распасціраецца ў даўжыню на цэлыя кіламетры). Але - запярэчыце вы, - 1000-я доля секунды яшчэ не сапраўдны ліліпут, як ніхто не назаве тысячу лікавым гігантам. Калі ўзяць мільённую долю секунды, то ўжо напэўна можна сцвярджаць, што гэта - велічыня нерэальная, прамежак часу, на працягу якога нічога адбыцца не можа.

Памыляецеся: нават і адна мільённая доля секунды - для сучаснага фізіка, напрыклад, - зусім не празмерна маленькі прамежак. У вобласці з'яў светлавых (і электрычных) навукоўцу даводзіцца мець справу з значна больш дробнымі часткамі секунды. Нагадаем перш за ўсё, што светлавы прамень прабягае штосекундна (у пустаце) 300.000 кіламетраў; такім чынам, у 1.000.000-ю долю секунды святло паспявае перанесціся на адлегласць 300 метраў - прыкладна на столькі ж, на колькі пераносіцца ў паветры гук на працягу цэлай секунды. Далей: святло ёсць з'ява хвалепадобнае, і лік светлавых хваляў, што праносяцца штосекундна праз кропку прасторы, вылічаецца сотнямі мільёнаў. Тыя светлавыя хвалі, якія, дзейнічаючы на ​​нашы вочы, выклікаюць адчуванне чырвонага святла, маюць частату ваганняў 400 мільёнаў у секунду; гэта значыць, што на працягу адной 1.000.000-й долі секунды ў нашы вочы  трапляе 400.000.000 хваляў, а адна хваля трапляе ў вока на працягу 400 000 000 000 000-й долі секунды.Вось сапраўдны лікавы ліліпут! Але гэты несумнеўны, рэальна існуючы ліліпут з'яўляецца сапраўдным волатам у параўнанні з яшчэ больш дробнымі долямі секунды, з якімі фізік сустракаецца пры вывучэнні рентгенавых прамянёў. Гэтыя дзіўныя прамяні, якія валодаюць уласцівасцю пранікаць праз многія непразрыстыя цела, уяўляюць сабою, як і бачныя прамяні, тую ж хвалепадобную з'яву, але частата ваганняў ў іх значна больш, чым у бачных: яна дасягае 25000 мільёнаў у секунду! Хвалі ідуць тут адна за адной у 60 разоў часцей, чым у промнях бачнага чырвонага святла.Прамяні "гама" і нядаўна адкрытыя "касмічныя" прамяні Геса валодаюць частатой яшчэ большаю, чым прамяні рэнтген. Значыць, і ў свеце ліліпутаў існуюць свае волаты і карлікі. Гулівер быў вышэй ліліпутаў усяго ў тузін раз і здаваўся ім волатам. Тут жа адзін ліліпут большы за другі ліліпута ў пяць тузінаў раз і, такім чынам, мае ўсе правы называцца ў адносінах да яго волатам. 

Ліліпуты прасторы

Цікава разгледзець цяпер, якія найменшыя адлегласці даводзіцца адмерваць і ацэньваць сучасным даследчыкам прыроды. У метрычнай сістэме мер найменшая адзінка даўжыні для штодзённага ўжывання – міліметр, яна прыкладна ўдвая менш таўшчыні запалкі. Каб вымяраць прадметы, бачныя простым вокам, такая адзінка даўжыні досыць дробная. Але для вымярэння бактэрый і іншых дробных аб'ектаў, адрозных толькі ў моцныя мікраскопы, міліметр залішне буйны. Навукоўцы звяртаюцца ў такіх вымярэннях да больш дробнай адзінкі - мікрона, які ў 1000 разоў менш міліметра. Так званыя чырвоныя крывяныя цельцы, якія налічваюцца дзесяткамі мільёнаў у кожнай кропельцы нашай крыві, маюць у даўжыню 7 мікронаў і ў таўшчыню 2 мікроны. Стос  з 1000 такіх цельцаў мае таўшчыню запалкі. Якім бы дробным не  здаецца нам мікрон, ён усё ж аказваецца празмерна буйным для адлегласцей, якія даводзіцца вымяраць сучаснаму фізіку. Драбнюткія, недаступныя нават мікраскопу часціцы, малекулы, з якіх складаецца рэчыва ўсіх цел прыроды, і якія складаюць іх яшчэ больш дробныя атамы маюць памеры ад адной 10000-ай да адной 1000-ай долі мікрона. Калі спыніцца на апошняй, найбольшай велічыні, то і тады акажацца, што мільён такіх макулінак (а мы ўжо ведаем, наколькі вялікі мільён), будучы размешчаны на адной прамой, ушчыльную адзін да аднаго, заняў бы ўсяго толькі адзін міліметр!

18. Гістарычная спраўка

Першым дробам, з якім пазнаёміліся людзі была палова. Наступным дробам была трэць. Старажытныя егіпцяне выкарыстоўвалі толькі адзінкавыя дробы 1/2, 1/3, 1/4, і гэтак далей, г.зн. дробы, лічнік якіх роўны 1. Усе вылічэнні з дробавымі лікамі выконваліся з дапамогай гэтых адзінкавых дробаў, што было вельмі складана. Таму вылічэнні маглі выконваць толькі адмыслова навучаныя пісцы. Доўгі час дзеянні з дробавымі лікамі лічыліся вельмі складанымі. Нездарма ў немцаў захаваўся выраз "Трапіць у дроб", што азначае "патрапіць" у тупік, у цяжкае становішча. Гэтая прымаўка нагадвае пра тыя часы, калі дробы, якія часам называлі ламанымі лікамі, лічылі самым цяжкім раздзелам матэматыкі. Таму чалавека, які ўмее выконваць дзеянні з дробамі лічылі разумным. 

Вусныя заданні:

1) Устаўце прапушчаны лік:

	?

Адказ: . Такія дробы называюцца ўзаемна-адваротнымі. 

Адказ: . 

Так малявалі дробы ў Старажытным Егіпце:

У Старажытным Кітаі замест рысы выкарыстоўвалі кропку: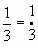

 Індыйцы дроб запісвалі так :.

 Сучасная форма запісу звычайных дробаў стала прымяняцца толькі ў 18 стагоддзі. Першым дробную рысу ўжыў арабскі вучоны Ал-Халар. У Еўропе дробную рысу для запісу звычайных дробаў выкарыстаў італьянскі матэматык Фібаначы.

19. Старадаўнія задачы на ​​дробы

1. Задача Эйлера.

Леанард Эйлер (4 красавіка 1707г.- 18 верасня 1783г.) - з'яўляецца заснавальнікам рускай навуковай матэматычнай школы. Поўны збор яго твораў налічвае больш за 70 тамоў, а спісы яго прац - больш за 850 назваў. 

Задача: Вырашыўшы ўсе свае зберажэннi падзяліць пароўну паміж усімі сынамі, бацька склаў завяшчанне. «Старэйшы з маіх сыноў павінен атрымаць 1000 рублёў і восьмую частку астатку; наступны - 2000 рублёў і восьмую частку новага астатку; трэці сын - 3000 рублёў і восьмую частку наступнага астатку і т. д. ». Вызначце лік сыноў і памер завешчанага зберажэння. 

Вядомы фізік А. В. Цінгер у сваіх успамінах пра Л. Н. Талстога распавядае аб наступнай задачы, якая вельмі падабалася вядомаму пісменніку:

2. «Арцелі касцоў трэба было скасіць два лугі, адзін удвая большы за другі. Палову дня арцель касіла вялікі луг. Пасля гэтага арцель падзялілася напалову: першая палова засталася на вялікім лузе і дакасіла яго да вечара да канца; другая ж палова касіла малы луг, на якім да вечара яшчэ застаўся ўчастак, скошаны на другі дзень касцамі за адзін дзень працы. Колькі касцоў было ў арцелі? »

 У пачатку XVIII стагоддзя ў Расіі было мала адукаваных людзей. Адным з аўтарытэтных навукоўцаў быў Лявонцій Піліпавіч Магніцкі, які ў 1703 годзе выдаў першы друкаваны падручнік па матэматыцы "Арыфметыка». Па гэтым падручніку навучаліся шматлікія пакаленні рускіх людзей. У кнізе Магніцкага шмат задач з розным зместам, уключаючы і дробы. 

3. «Адзін чалавек вып'е кадзь піцця ў 14 дзён, а з жонкаю вып'е тую ж кадзь у 10 дзён. За колькі  дзён жонка яго вып'е тую ж кадзь ?»

Падарожнік, дагнаўшы іншага, спытаў: «Як далёка да вёскі, якая ў нас наперадзе?». Прамовіў другі падарожнік: "Адлегласць ад той вёскі, ад якой ты ідзеш, роўна трэцяй частцы ўсёй  адлегласці паміж вёскамі, а калі яшчэ пройдзеш тры вярсты, тады будзеш роўна пасярэдзіне паміж вёскамі». Колькі вёрст засталося прайсці першаму падарожніку?