1. Лікі і лічбы
Лічбы - адно з самых старажытных вынаходстваў. З лічбаў складваюцца лікі: маленькія, вялікія і вельмі вялікія. Але ці заўсёды было так? Ці ва ўсе часы і ці ва ўсіх народаў?

 Для таго каб адлюстраваць, напрыклад, цэлы лік 23.145, дастаткова запісаць у шэраг два іерогліфы, якія паказваюць дзесяць тысяч, затым тры іерогліфы для тысячы, адзін - для ста, чатыры - для дзесяці і пяць іерогліфаў для адзінкі:
Для таго каб адлюстраваць, напрыклад, цэлы лік 23.145, дастаткова запісаць у шэраг два іерогліфы, якія паказваюць дзесяць тысяч, затым тры іерогліфы для тысячы, адзін - для ста, чатыры - для дзесяці і пяць іерогліфаў для адзінкі:
 Гэтага аднаго прыкладу дастаткова, каб навучыцца запісваць лікі так, як іх малявалі старажытныя егіпцяне. Гэта сістэма вельмі простая і прымітыўная.
Гэтага аднаго прыкладу дастаткова, каб навучыцца запісваць лікі так, як іх малявалі старажытныя егіпцяне. Гэта сістэма вельмі простая і прымітыўная.
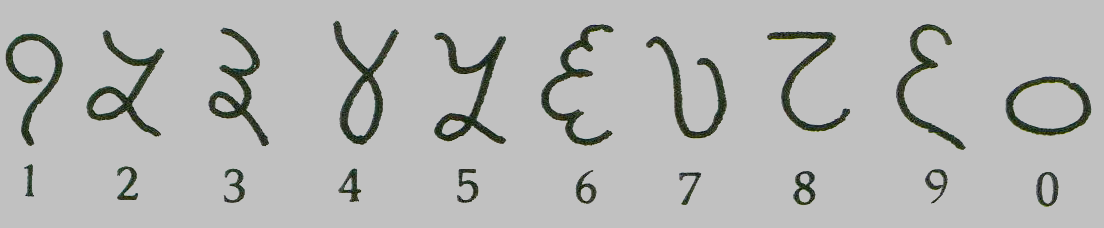 Аднак Індыя была адарваная ад іншых краін, - на шляху ляжалі тысячы кіламетраў адлегласці і высокія горы.
Аднак Індыя была адарваная ад іншых краін, - на шляху ляжалі тысячы кіламетраў адлегласці і высокія горы.


Натуральныя лікі.
3. Фігурныя лікі

 Даўным - даўно, дапамагаючы сабе пры ліку каменьчыкамі, людзі звярталі ўвагу на правільныя фігуры, якія можна выкласці з каменьчыкаў. Можна проста класці каменьчыкі ў рад: адзін, два, тры. Калі класці іх у два рады, каб атрымліваліся прамавугольнікі, мы ўбачым, што атрымліваюцца ўсе цотныя лікі. Можна выкладваць камяні ў тры рады: атрымаюцца лікі, якія дзеляцца на тры. Кожны лік, які на што-небудзь дзеліцца, можна прадставіць такім прамавугольнікам, і толькі простыя лікі не могуць быць "прамавугольнымі". Аказваецца, што існуюць лікі, якія можна выкладваць у выглядзе геаметрычных тэл. Гэта - цялесныя лікі (прасторавыя фігурныя лікі).
Даўным - даўно, дапамагаючы сабе пры ліку каменьчыкамі, людзі звярталі ўвагу на правільныя фігуры, якія можна выкласці з каменьчыкаў. Можна проста класці каменьчыкі ў рад: адзін, два, тры. Калі класці іх у два рады, каб атрымліваліся прамавугольнікі, мы ўбачым, што атрымліваюцца ўсе цотныя лікі. Можна выкладваць камяні ў тры рады: атрымаюцца лікі, якія дзеляцца на тры. Кожны лік, які на што-небудзь дзеліцца, можна прадставіць такім прамавугольнікам, і толькі простыя лікі не могуць быць "прамавугольнымі". Аказваецца, што існуюць лікі, якія можна выкладваць у выглядзе геаметрычных тэл. Гэта - цялесныя лікі (прасторавыя фігурныя лікі).
 (лінейны лік 5)
(лінейны лік 5)
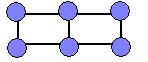 (плоскі лік 6)
(плоскі лік 6)
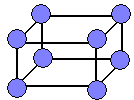 (аб’ёмны лік 8)
(аб’ёмны лік 8)
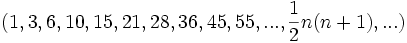


 (пяцівугольныя лікі 12, 5)
(пяцівугольныя лікі 12, 5)

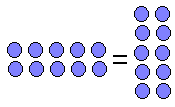


Лічэнне на каменьчыках пакінула глыбокі след у гісторыі матэматыкі. Старажытныя грэкі, калі ім даводзілася памнажаць лікі, малявалі прамавугольнікі, вынікам множання трох на пяць быў прамавугольнік са старанамі тры і пяць. Гэта - развіццё лічэння на каменьчыках. Мноства заканамернасцей, якія ўзнікаюць пры дзеяннях з лікамі, былі выяўленыя старажытнагрэчаскімі вучонымі пры даследаванні чарцяжоў. І доўгія стагоддзі лепшым пацвярджэннем справядлівасці такіх суадносін лічыўся спосаб геаметрычны, з прамавугольнікамі, квадратамі, пірамідамі і кубамі.
Лічбы - адно з самых старажытных вынаходстваў. З лічбаў складваюцца лікі: маленькія, вялікія і вельмі вялікія. Але ці заўсёды было так? Ці ва ўсе часы і ці ва ўсіх народаў?
- Спачатку лічылі на пальцах.
Не так ужо і шмат даводзілася лічыць першабытнаму чалавеку. Быў у яго свой першабытны «камп’ютар» - дзесяць пальцаў на руках. Разгінаў пальцы, складваў лікі. Загінаў - аднімаў. На пальцах лічыць зручна, толькі вынік вылічэнняў захоўваць нельга. Не будзеш жа цэлы дзень хадзіць з загнутымі пальцамі. Гэты старажытны «прыбор» дагэтуль ужываюць маленькія дзеці, калі пачынаюць вучыцца лічыць у межах дзесяці. Спачатку лічылі на пальцах. Калі пальцы на адной руцэ заканчваліся, пераходзілі на іншую, а калі на двух руках не хапала, пераходзілі на ногі. Таму, калі ў тыя часы хтосьці хваліўся, што ў яго «дзве рукі і адна нага курэй», гэта азначала, што ў яго пятнаццаць курэй, а калі гэта называлася «ўвесь чалавек», гэта значыць дзве рукі і дзве нагі. Яшчэ нядаўна існавалі плямёны, у мове якіх былі назвы толькі двух лікаў: «адзін» і «два». Пяць - рука, шэсць - адзін на другой руцэ, сем - два на другой руцэ, дзесяць - дзве рукі, паўчалавека. Пятнаццаць - нага, шаснаццаць - адзін на іншай назе, дваццаць - адзін чалавек, дваццаць два - два на руцэ іншага чалавека, сорак - два чалавекі, пяцьдзясят тры - тры на першай назе ў трэцяга чалавека. Раней людзі каб пералічыць статак з 128 аленяў павінны былі ўзяць сем чалавек.
2. Выкарыстанне камянёў, вузельчыкаў.
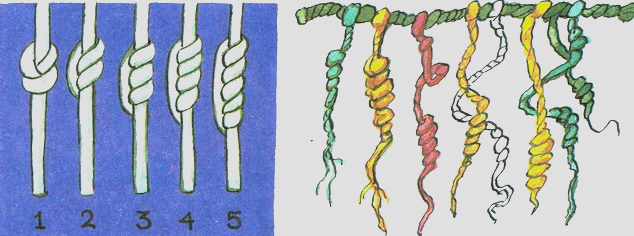
Старажытны чалавек здагадаўся: для лічэння можна выкарыстоўваць не толькі пальцы, але і ўсе, што трапляецца пад рукі - каменьчыкі, палачкі, костачкі ... У старажытныя часы, калі чалавек хацеў паказаць, колькімі жывёламі ён валодаў, ён клаў у вялікі мех столькі каменьчыкаў, колькі ў яго было жывёл. Чым больш жывёл, тым больш каменьчыкаў. Адсюль і з’явілася слова «калькулятар», «калькулюс» па лацінску азначае «камень». Перуанскія інкі вялі лічэнне жывёл і ўраджаю, завязваючы вузельчыкі на раменьчыках або шнурках рознай даўжыні і колеру. Гэтыя вузельчыкі называліся стос. У некаторых багацеяў запасіцца па некалькі метраў гэтай вяровачнай «падліковай кнігі», паспрабуй, успомні праз год, што азначаюць 4 вузельчыкі на шнурку! Таму таго, хто завязваў вузельчыкі, называлі ўспамінальнікам.
3. Старажытныя шумеры
Першымі прыдумалі запіс лікаў старажытныя шумеры. Яны карысталіся ўсяго двума лічбамі. Вертыкальная рысачка азначала адну адзінку, а вугал з двух ляжачых рысачак - дзесяць. Гэтыя рысачкі ў іх атрымліваліся ў выглядзе клінаў, таму што яны пісалі вострай палачкай на сырых гліняных дошчачках, якія потым сушылі і абпальвалі. Вось так выглядалі гэтыя дошчачкі.
Пасля лічэння па засечках людзі вынайшлі асаблівыя сімвалы, названыя лічбамі. Яны сталі прымяняцца для абазначэння розных лікаў якіх-небудзь прадметаў. Розныя цывілізацыі стваралі свае ўласныя лічбы
4. Егіпецкая нумералогія
Так, напрыклад, у старажытнай егіпецкай нумарацыі, якая зарадзілася больш за 5000 гадоў таму, існавалі адмысловыя знакі (іерогліфы) для запісу лікаў 1, 10, 100, 1000, ...:
5. Народы (вавіланяне, асірыйцы, шумеры), якія жылі ў Міжрэччы Тыгра і Еўфрата ў перыяд ад II тысячагоддзя да н.э. і да пачатку нашай эры, спачатку пазначалі лікі з дапамогай колаў і паўколаў рознай велічыні, але затым сталі выкарыстоўваць толькі два клінапісныя знакі. Прамы клін ▼ і ляжачы клін ◀. Гэтыя народы выкарыстоўвалі шасцідзесяцярычную сістэму злічэння, напрыклад лік 23 малявалі так: ◀ ◀ ▼▼▼ . Лік 60 зноў пазначаўся знакам ▼. Напрыклад лік 92 запісвалі так: ▼◀◀◀▼▼ .
6. Індзейцы племя Майя У пачатку нашай эры індзейцы племя Майя, якія жылі на паўвостраве Юкатан у Цэнтральнай Амерыцы, карысталіся іншай сістэмай злічэння - дваццацярычнай. Яны пазначалі 1 кропкай, а 5 - гарызантальнай рысай, напрыклад, запіс ‗‗‗‗‗‗ азначала 14. У сістэме злічэння Майя быў і знак для нуля. Па сваёй форме ён нагадваў напаўзачыненае вока.
7. У Старажытнай Грэцыі спачатку лікі 5, 10, 100, 1000, 10000 пазначалі літарамі Г, Н, Х, М, а лік 1 - рысачкай /. △ △ △ Г (35) і г.д. З гэтых знакаў складалі абазначэнні. Пазней лічбы 1, 2, 3, 4, 5, 6, 7, 8, ... сталі пазначаць літарамі грэчаскага алфавіту, да якога прыйшлося дадаць яшчэ тры састарэлыя літары. Каб адрозніць лічбы ад літар, над літарамі ставілі рысачку.
8. Старажытныя індыйцы вынайшлі для кожнай лічбы свой знак. Вось як яны выглядалі :
9.Арабы былі першымі «чужымі», якія запазычылі лічбы ў індыйцаў і прывезлі іх у Еўропу. Крыху пазней арабы спрасцілі гэтыя значкі, яны сталі выглядаць вось так
Яны падобныя на многія нашы лічбы. Слова «лічба» таксама дасталася нам ад арабаў па спадчыне. Арабы нуль, або «пуста», называлі «сіфра». З тых часоў і з'явілася слова «лічба» - цыфра.
10. Рымская нумарацыя. У аснове рымскай нумарацыі выкарыстаны прынцыпы складання (напрыклад, VI = V + I) і аднімання (напрыклад, IX = X -1). Рымская сістэма нумарацыі дзесятковая, але непазіцыйная. Рымскія лічбы утварыліся не ад літар. Першапачаткова яны пазначаліся, як і ў многіх народаў, «палачкамі» (I - адзін, X - 10 - перакрэсленая палачка, V - 5 - палова ад дзесяці, сто - кружочак з рысачкай ўнутры, пяцьдзесят - палова гэтага знака і т. д.). З часам некаторыя знакі змяніліся: С - сто, L - пяцьдзесят, М - тысяча, D - пяцьсот. Напрыклад:
XL - 40, LXXX - 80, ХС - 90,
CDLIX - 459, CCCLXXXII - 382, CMXCI - 991,
MCMXCVIII - 1998 MMI - 2001
Адбылося паступовае ператварэнне першапачатковых лічбаў у нашы сучасныя лічбы.
11. Лічбы рускага народа. Арабскія лічбы ў Расіі сталі ўжываць, у асноўным, з XVIII стагоддзя. Да таго нашы продкі выкарыстоўвалі славянскую нумарацыю. Над літарамі ставіліся цітламі (рысачкі), і тады літары азначалі лікі. У адным з рускіх рукапісаў XVIII стагоддзя напісана: «... Знай же то, что есть сто и что есть тысяща, и что есть тма, и что есть легион, и что есть леодр...; ... сто есть десятью десять, а тысяща есть десять сот, а тма десять тысящ, а легион есть десять тем, а леодр есть десять легионов...».. Сотні мільёнаў называліся «калодамі». Першыя дзевяць лікаў запісваліся так

Натуральныя лікі.
Для лічэння прадметаў ужываюць натуральныя лікі. Любы натуральны лік можна запісаць з дапамогай дзесяці лічбаў: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Напрыклад: трыста дваццаць восем - 328,
пяцьдзесят тысяч чатырыста дваццаць адзін - 50421.
Такі запіс лікаў называюць дзесятковым.
Паслядоўнасць усіх натуральных лікаў называюць натуральным радам:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, .. .
Самы маленькі натуральны лік - адзінка (1). У натуральным радзе кожны наступны лік на 1 больш папярэдняга. Натуральны рад бясконцы, найбольшага ліку ў ім няма.
Значэнне лічбы залежыць ад яе месца ў запісе ліку.
Напрыклад 375: лічба 5 азначае 5 адзінак, яна на апошнім месцы ў запісе нумару (у разрадзе адзінак), лічба 7 - дзясяткі, яна знаходзіцца на перадапошнім месцы (у разрадзе дзясяткаў), лічба 3 - сотні, яна стаіць на трэцім месцы ад канца (у разрадзе сотняў) і т. д.
Лічба 0 азначае адсутнасць адзінак дадзенага разраду ў дзесятковым запісе. Яна служыць і для абазначэння ліку "нуль". Гэты лік азначае "ніводнага". Памятайце! Нуль не адносяць да натуральных лікаў.
Калі запіс натуральнага ліку складаецца з аднаго знаку - адной лічбы, то яго называюць адназначным. Напрыклад, лікі 1, 5, 8 - адназначныя.
Калі запіс ліку складаецца з двух знакаў - двух лічбаў, то яго называюць двухзначны. Лікі 14, 33, 28, 95 - двухзначныя, лікі 386, 555, 951 - трохзначныя, лікі 1346, 5787, 9999 - чатырохзначныя і т.
2. Лікі – веліканы
2. Лікі – веліканы
Яшчэ ў старажытнасці матэматыкі запісвалі вельмі вялікія лікі і прыдумвалі назвы для іх.
Мы зараз выкарыстоўваем пры запісе лікаў класы адзінак, сотняў і мільёнаў. А як называецца наступны клас? Запішам лік, у якім сем разрадаў, напрыклад 1 000 000 - адзін мільён. Тэрмін «мільён» упершыню з'явіўся ў Італіі, першае згадванне датуецца 1250 г.
Дапішам справа яшчэ тры нулі, атрымаем лік адзін мільярд. Слова «мільярд» упершыню упамінаецца ў 1558 г. і выкарыстоўвалася для абазначэння ліка, у якім за адзінкай запісвалася дванаццаць нулёў. Зараз гэта 1 000 000 000. Дапісваючы справа па тры нулі, мы кожны раз будзем атрымліваць у ліку яшчэ адзін клас. У розных краінах да гэтага часу адны і тыя ж назвы выкарыстаюць для розных па колькасці класаў лікаў. Не існуе яшчэ адзінай сістэмы назваў для вялікіх лікаў. Напрыклад, у Амерыцы і Францыі тысяча міліёнаў (1 000 000 000) - гэта біліён, або мільярд. У Германіі і Англіі біліён - гэта міліён міліёнаў, г.зн. 1 з наступнымі дванаццаццю нулямі. Прадаўжаючы дапісваць па тры нулі, матэматыкі атрымлівалі ўсё новыя вялікія ліку: квадрыльён (1 з пятнаццацю нулямі), квінтэлльён (1 з васемнаццаццю нулямі), секстыльён (1 з дваццацi адным нулём), септыльён (1 з дваццацi чатырма нулямі), актыльён (1 з дваццаць сям'ю нулямі) ... Ёсць назва нават для ліку, у якім пасля адзінкі запісана сто нулёў, - гэта гугал. Чалавецтва працягвае павялічваць разраднасць лікаў і прыдумляць ім новыя назвы. Для ліку, у якім пасля адзінкі запісана трыста тры нулі, таксама ёсць назва - гэта центыльён. З цягам часу людзі навучыліся не толькі называць і абазначаць лікі, але і выконваць з імі арыфметычныя дзеянні.
Фігурныя лікі былі вядомыя яшчэ ў глыбокай старажытнасці. Мяркуюць, што ўпершыню яны з'явіліся ў VI стагоддзі да нашай эры - у школе Піфагора. У далейшым многія матэматыкі цікавіліся гэтымі лікамі. Пра іх даказана шмат важных і складаных тэарэм.
Лікі старажытнымі грэкамі, а разам з імі Піфагорам і піфагарэйцамі, прадстаўляліся ў выглядзе каменьчыкаў, раскладзеных на пяску або на падліковай дошцы - абаку. Па гэтай прычыне грэкі не ведалі нуля, бо яго немагчыма было "убачыць". Але і адзінка яшчэ не была паўнапраўным лікам, а ўяўлялася як нейкі "лікавы атам", з якога ўтвараліся ўсе лікі. Піфагарэйцы называлі адзінку "мяжой паміж лікам і часткамі", г.зн. паміж цэлымі лікамі і дробамі, але ў той жа час бачылі ў ёй "насенне і вечны корань". Лік жа вызначаўся як мноства, складзенае з адзінак. Асаблівае становішча адзінкі як "лікавага атаму", радніла яе з пунктам, які лічыўся "геаметрычным атамам". Вось чаму Арыстоцель пісаў: "Пункт ёсць адзінка, якая мае становішча, адзінка ёсць пункт без становішча". Т.ч. , піфагарыйскія лікі ў сучаснай тэрміналогіі - гэта натуральныя лікі.
Лічбы-каменьчыкі раскладваліся ў выглядзе правільных геаметрычных фігур, гэтыя фігуры класіфіцыраваліся. Так з’явіліся лікі, сёння названыя фігурнымі.
Такім чынам, фігурныя лікі - агульная назва лікаў, геаметрычнае прадстаўленне якіх звязана з той ці іншай геаметрычнай фігурай.
Адрозніваюць наступныя віды фігурных лікаў:
Лінейныя лікі (г.зн. простыя лікі) - лікі, якія дзеляцца толькі на адзінку і на саміх сябе і, такім чынам, прадстаўленыя ў выглядзе паслядоўнасці пунктаў, выбудаваных у лінію (1,2, 3,5,7,11,13,17,19,23, ...):
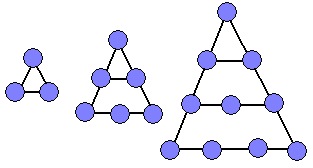
Плоскія лікі - лікі, прадстаўленыя ў выглядзе здабытку двух множнікаў (4,6,8,9, 10,12,14,15, ...):
Аб’ёмныя лікі, выяўляюцца здабыткам трох множнікаў (8,12,18,20,24,27,28, ...):
Трохвугольныя лікі:
(трохвугольныя лікі 3,6,10)
Квадратныя лікі - (1,4,9,16,25,36,49,64,81,100, ..., n2, ...) выяўляюцца здабыткам двух аднолькавых лікаў, г.зн. з'яўляюцца поўнымі квадратамі.
(Квадратныя лікі 4,9,16)
Пяцівугольныя лікі:
Кубічныя лікі.
Вельмі цікавыя кубічныя лікі, якія ўзнікаюць пры складанні кубікаў:
1) 2 * 2 * 2 = 8 (два паверхі з квадратаў 2 * 2
2). 3 * 3 * 3 = 27 (тры паверхі з квадратаў 3 * 3
3) 4 * 4 * 4 = 64 (чатыры паверхі з квадратаў 4 * 4
4) 5 * 5 * 5 = 125, 6 * 6 * 6 = 216, 7 * 7 * 7 = 343, 8 * 8 * 8 = 512, 9 * 9 * 9 = 729, 10 * 10 * 10 = 1000 і гэтак далей. Зараз зразумела, чаму пра такія лічбы кажуць: "два ў кубе", "тры ў кубе", "дзесяць у кубе"?
Пірамідальная лікі ўзнікаюць пры складанні круглых каменьчыкаў горкай так, каб яны не рассыпаліся. Атрымліваецца піраміда. Кожны пласт у такой пірамідзе - трохвугольны лік. Наверсе адзін каменьчык, пад ім - 3, пад тымі - 6 і г.д .: 1, 1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20, ...
Фігурнае прадстаўленне лікаў дапамагало піфагарэйцам адкрываць законы арыфметычных аперацый, а таксама лёгка пераходзіць да лікавай характарыстыкі геаметрычных аб'ектаў - вымярэнні плошчаў і аб'ёмаў. Так, прадстаўляючы лік 10 у двух формах: 5 * 2 = 2 * 5, лёгка "убачыць" перамяшчальную ўласцівасць множання:
a * b = b * a.
У тым жа ліку 10: (2 + 3) * 2 = 2 * 2 + 3 * 2 = 10 можна "разгледзіць" і размеркавальную ўласцівасць складання адносна множання: (a + b) c = ac + bc.
Нарэшце, калі "каменьчыкі", якія ўтвараюць фігурныя лікі, прадставіць у выглядзе роўных па плошчы квадрацікаў, то, укладваючы іх у прамавугольны лік ab: аўтаматычна атрымліваем формулу для вылічэння плошчы прамавугольніка:
S = ab.
П'ер Ферма выявіў, напрыклад, што
а) усякі натуральны лік ёсць трохвугольны лік, або сума двух або трох трохвугольных лікаў;
б) усякі натуральны лік ёсць квадрат, або сума двух, трох ці чатырох квадратных лікаў;
в) усякі натуральны лік ёсць пяцівугольны лік, або сума двух, трох, чатырох ці пяці пяцівугольных лікаў;
г) навогул, любы натуральны лік можа быць прадстаўлены ў выглядзе сумы не больш чым k k-вугольных лікаў.
Лічыцца, што менавіта ад фігурных лікаў пайшоў выраз «Узвядзенне ў квадрат або куб».
Паглядзіце: 1 + 3 = 4 (г.зн. 22), 3 + 6 = 9 (г.зн. 32), 6 + 10 = 16 (г.зн. 42) і г.д.
Лічэнне на каменьчыках пакінула глыбокі след у гісторыі матэматыкі. Старажытныя грэкі, калі ім даводзілася памнажаць лікі, малявалі прамавугольнікі, вынікам множання трох на пяць быў прамавугольнік са старанамі тры і пяць. Гэта - развіццё лічэння на каменьчыках. Мноства заканамернасцей, якія ўзнікаюць пры дзеяннях з лікамі, былі выяўленыя старажытнагрэчаскімі вучонымі пры даследаванні чарцяжоў. І доўгія стагоддзі лепшым пацвярджэннем справядлівасці такіх суадносін лічыўся спосаб геаметрычны, з прамавугольнікамі, квадратамі, пірамідамі і кубамі.
Комментариев нет:
Отправить комментарий