В мире математических парадоксов

Исчезновение клетки

Существует множество задач на перестановку фигур, обладающих признаками софизмов: изначально в их условие введена замаскированная ошибка. В какой-то мере данные задачи ближе к оптическим иллюзиям, чем к математике.

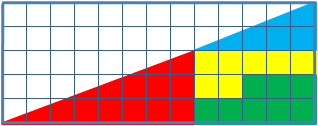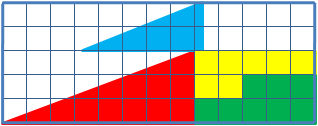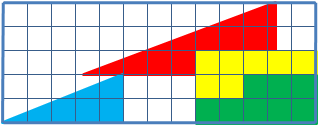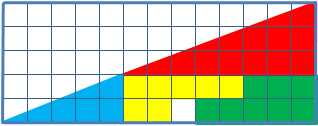 Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка. 

Математически парадоксов и таинственного исчезновения площади тут нет. Визуально наблюдаемые треугольники, на самом деле таковыми не являются, гипотенузы в обоих псевдо треугольниках на самом деле являются ломаными линиями (в первом треугольнике она с изломом внутрь, а во втором — наружу). Если наложить треугольник друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «пропавшая» площадь.

Парадокс Тесея

   «Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?»

Было предложено несколько решений этого парадокса. Согласно философской школе Аристотеля существует несколько описывающих объект причин: форма, материал и суть вещи (которая, по учению Аристотеля, является самой важной характеристикой). Исходя из этого корабль остался тем же, так как его суть не поменялась, лишь изменился износившийся материал. В следующем решении предложили дать аргументу «ту же» количественную и качественную характеристику. В таком случае, после смены досок корабль  окажется количественно тем же, а качественно — уже другим кораблём.

Парадокс Абилина

Данный парадокс заключается в том, что группа людей может принять решение, противоречащее возможному выбору любого из членов группы из-за того, что каждый индивидуум считает, что его цели противоречат целям группы, а потому не возражает.

   В один жаркий вечер некая семья играла в домино на крыльце до тех пор, пока тесть не предложил съездить в город отобедать. Жена сказала: «Звучит неплохо». Муж, несмотря на то, что поездка обещала быть долгой и жаркой, подумал, что надо бы подстроиться под других, и произнёс: «По-моему, неплохо; надеюсь, что и твоя мама не откажется». Тёща же ответила: «Конечно, поехали! Я не была в городе уже давно».

Дорога была жаркой, пыльной и долгой. Когда же они наконец приехали в кафетерий, еда оказалась невкусной. Спустя четыре часа они, измученные, вернулись домой.
Один из них произнёс неискренне: «Верно, неплохая была поездка?». Тёща на это сказала, что, на самом деле, она бы лучше осталась бы дома, но поехала, раз уж остальные трое были полны энтузиазма. Муж сказал: «Я был бы рад никуда не ездить, поехал лишь чтобы доставить остальным удовольствие». Жена произнесла: «А я поехала, рассчитывая на радость остальных. Надо было быть сумасшедшим, чтобы добровольно отправиться в эту поездку». Тесть ответил, что он предложил это лишь потому, что ему показалось, что остальным скучно.

И они сидели, ошеломлённые тем, что поехали в поездку, которой никто из них не хотел. Каждый из них предпочёл бы спокойно наслаждаться тем днём.

Думаю что многие не раз сталкивались с данным парадоксом и в своей жизни.

 Парадокс лжеца

  Верно то, что оно — ложно;  но если оно — ложно, тогда то, что оно утверждает, неверно; значит, неверно, что утверждение на картинке — ложно, и, значит, это утверждение истинно.

 Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно и истинно и ложно. В рамках формальной логики данное утверждение не доказуемо и неопровержимо, поэтому решения данного парадокса не существует, но существуют различные варианты его устранения.

Для этого можно применить рассуждение, для этого положим, что утверждение истинно на 0,5, тогда оно и ложно на 0,5, то есть не всякую фразу можно назвать целиком ложной или целиком истинной — «в чем-то высказывание на картинке лжёт, а в чем-то — говорит правду»

Парадокс кучи и парадокс «Лысого». 

 Данные парадоксы известны ещё с древности.

   «Если к одному зерну добавлять по зёрнышку, то в какой момент образуется куча?»

или обратная формулировка: «удаляя из кучи в 1 млн зёрен по одному зёрнышку, с какого момента она перестаёт быть кучей?»

 Парадокс основан на очевидной предпосылке, согласно которой одно зёрнышко не образует кучи, и индуктивной предпосылке, по которой добавление одного зёрнышка к совокупности, кучей не являющейся, несущественно для образования кучи. Из этих предпосылок следует, что никакая совокупность из сколь угодно большого количества зёрен не будет образовывать кучи, что противоречит представлению о существовании кучи из зёрен. Очевидно, что эти рассуждения приводят к неправильным выводам.

Аналогичные рассуждения можно применить и к парадоксу «Лысого»:

  «Если волосы с головы выпадают по одному, с какого момента человек становится лысым?»